Изучение аддитивной комбинаторики продолжается в этом семестре в форме
семинара. Читаем и обсуждаем самое интересное и актуальное.
Новый подход к неравенствам Плюннеке, аналитическая форма леммы
регулярности Семереди, свежие успехи в применении анализа Фурье и все
остальное.

Руководитель семинара Ф. В. Петров, знакомство с читавшимся в прошлом
семестре курсом желательно, но не обязательно.

Время и место занятий в стадии обсуждения.



=================
Аддитивная комбинаторика
Лектор — Ф.В. Петров (ПОМИ)
Начало - вторник 6 марта 17:00 ауд 203 ПОМИ

Аддитивная комбинаторика изучает комбинаторные свойства аддитивных групп целых чисел и конечных полей. Сюда относится, например, знаменитая теорема Ван дер Вардена: если натуральные числа покрашены в конечное количество цветов, то найдется сколь угодно длинная одноцветная арифметическая прогрессия. Глубоким усилением теоремы Ван дер Вардена является теорема Семереди: для всяких 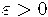и натурального 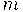при достаточно большом натуральном 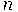любое множество, состоящее из 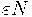натуральных чисел, меньших 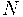, содержит арифметическую прогрессию длины 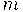. Известно много доказательств теоремы Семереди, использующих как чисто комбинаторные соображения (как в исходном доказательстве Семереди), так и аппарат эргодической теории (подход Фюрстенберга). Эта область бурно развивается в последние тридцать лет. Одним из самых звонких ее достижений является теорема Грина-Тао о существовании сколь угодно длинной арифметической прогрессии, состоящей из простых чисел. Мы постараемся познакомиться по крайней мере с основными идеями, а если хватит сил — то и с деталями доказательств.

Другая тема, которую хочется затронуть в курсе — свойства сумм вычетов по простому модулю. Отправной точкой тут служит теорема Коши-Дэвенпорта: для множеств 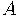, 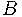вычетов по модулю простого числа 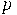множество 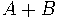имеет хотя бы 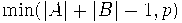элементов. В настоящее время здесь применяются комбинаторные, алгебраические (Combinatorial Nullstellensatz Ноги Алона), аналитические (гармонический анализ) методы.

• Professor: Федор Петров