Н. Калинин, "Дифференциальная топология"
Начало 5 октября, вторник, 19:30, ауд 106.
Дифференциальная топология является одним из общих мест в математике, в ней формализуются утверждения такого типа: "В 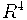две поверхности в общем положении пересекаются по набору точек", "Практически любое отображение окружности в 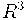является вложением".
Дифференциальная топология предоставляет аппарат для доказательства таких, почти очевидных, утверждений, встречающихся в топологии сплошь и рядом.
Вместе с тем, дифференциальная топология и сейчас является одной из бурно развивающихся областей математики.

Программа:

1. Многообразия, многообразия с краем, касательное расслоение.
2. Вложения и погружения. Теорема Уитни о вложениях.
3. Функциональные пространства.
4. Трансверсальность, теорема Морса-Сарда.
5. Векторные расслоения и трубчатые окрестности.
6. Степени отображений, индексы пересечения и эйлерова
характеристика.
7. Связность и кривизна в касательном расслоении.
8. Дифференциальные формы на многообразиях. Когомологии де Рама.

Основные источники знаний : М.Хирш, "Дифференциальная топология", С.М.
Гусейн-Заде "Дифференциальная геометрия".

Pre-requirements: общая топология, теорема о неявной функции