Периодические дифференциальные операторы. Спектральные свойства
и усреднение.

Т. А. Суслина (СПбГУ, физфак)

Продолжение курса в весеннем семестре 19 февраля в 17:00 ауд 203 ПОМИ


Курс рассчитан на студентов математических и физических специальностей,
начиная с 3 курса, и аспирантов. Необходимо знание основ анализа (включая ряды Фурье, преобразование Фурье, аналитические функции). Желательно знакомство с теорией меры и интеграла Лебега, с основами функционального анализа и спектральной теории операторов.

В течение ноября и декабря 2010 г. предполагается дать введение в спектральную
теорию периодических дифференциальных операторов. Основное внимание уделяется многомерному
случаю (операторам в 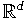). Во втором семестре планируется
продолжение курса, в основном посвященное новому теоретико-операторному подходу
к задачам теории усреднений (гомогенизации) периодических дифференциальных операторов.


Дифференциальные операторы с коэффициентами, периодически зависящими от координат,
возникают во многих задачах математической физики (в акустике, теории упругости, теории твердого тела,
электродинамике, и т.~д.). Например, движение электрона в кристалле описывается
оператором Шредингера с периодическим потенциалом.
Для современных прикладных областей периодические операторы также имеют важное значение
(фотонные кристаллы, композитные материалы, и пр.)
Курс знакомит с основами теории периодических дифференциальных операторов в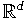
и их спектральными свойствами.

Примерный план лекций в 1 семестре

• Решетки в 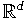. Периодические функции. Ряды Фурье.
• Преобразование Гельфанда.
• Разложение периодических дифференциальных операторов в прямой интеграл.
• Зонная структура спектра. Зонные функции. Их свойства.
• Перекрытие зон. Гипотеза Бете-Зоммерфельда (обзор).
• Проблема отсутствия вырожденных спектральных зон (проблема абсолютной непрерывности спектра) для периодического оператора Шредингера.
• Пороговые свойства периодических дифференциальных операторов. Применение к теории усреднений в пределе малого периода.