Е. Степанов, "Минимальные поверхности -I" (с/к лаборатории им. П.Л. Чебышева СПбГУ)
(MinSurf)
Курс лекций «Минимальные поверхности-I» (2 семестр, 16-18 часов)
Евгений Степанов, СПбГУ и СПбГУ ИТМО
Первая лекция во вторник 22 февраля в 17:30 на 14 линии д.29
Аннотация.
Курс задуман как элементарное введение в современную геометрическую теорию меры как теорию, сложившуюся вокруг задачи о минимальных поверхностях (задачи Плато) - задачи о том, как выглядит (какую форму принимает) мыльная пленка, образованная на проволочной рамке заданной формы. В первой части курса рассматриваются вопросы постановки задачи об «обобщенных» минимальных поверхностях. Таких обобщений придумано много (потоки, варифолды, (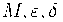 )-
)-
Содержание курса
1.Справочные сведения из геометрической теории меры. Липшицевы функции, спрямляемые множества, касательные пространства к мерам, [кривизна мер, размерность мер и свойства спрямляемости мер]. Минимальные поверхности: конкретные примеры.
2.Потоки Уитни в конечномерном евклидовом пространстве. Формы, потоки, нормальные потоки, спрямляемые потоки, плоские цепи. Массы потоков. Потоки со значениями в различных группах (в т.ч. целочисленные).
3.Потоки в метрическом пространстве (конструкция De Giorgi-Ambrosio-Kirchheim’а). Нормальные и спрямляемые потоки. Евклидовы плоские цепи иметрические потоки. Топологии в пространствах потоков.
4.Сечения потоков. Теоремы о спрямляемости.
5.Компактность. Сходимость Громова-Хаусдорфа.
6.Изопериметрические неравенства. Конусы.
7.Существование решений задачи Плато в метрическом пространстве.
8.Примеры минимальных поверхностей. Краткий обзор результатов о регулярности минимальных поверхностей