 | Differential Geometry Seminar on Generalized Complex Geometry |
|
Differential Geometry Seminar on
Generalized Complex Geometry venue SPbU, Dept. of Mathematics & Computer Science time TBDorganizer Casey Blacker (cblacker271@gmail.com) PDMI coordinator Sylvain Lavau (lavau@math.univ.lyon1.fr)
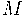
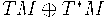
 on a smooth manifold  is an assignment to each fiber of theextended tangent bundle  of a linear complex structure in a locally compatible manner. Theresulting formalism extends both complex and symplectic geometry, and was introduced in 2003 by Nigel Hitchin with an eye to string theory. The aim of this learning seminar is first to review the foundational material, and then to acquaint ourselves with the state of the art and open questions. Related constructions include, • Lie algebroids • Dirac structures • Courant brackets • moment maps • generalized K ̈ahler structures • T-duality This seminar should appeal to students and researchers with interests in differential geometry and mathematical physics.
• Gil Cavalcanti. Introduction to generalized complex geometry. Publica ̧c ̃oes Matem ́aticas do IMPA. Instituto Nacional de Matem ́atica Pura e Aplicada (IMPA), Rio de Janeiro, 2007. 26o Col ́oquio Brasileiro de Matem ́atica, https://impa.br/wp-content/uploads/2017/04/26CBM_05.pdf • Marco Gualtieri. Generalized complex geometry. PhD thesis, University of Oxford, November 2003, https://arxiv.org/abs/math/0401221 • Nigel Hitchin. Lectures on generalized geometry. In Surveys in differential geometry. Volume XVI. Geometry of special holonomy and related topics, volume 16 of Surv. Differ. Geom., pages 79–124. Int. Press, Somerville, MA, 2011 • Nigel Hitchin. Generalized Calabi-Yau manifolds. Q. J. Math., 54(3):281–308, 2003, https://proxy.library.spbu.ru:2060/10.1093/qmath/hag025 Physical references: • Paul Koerber. Lectures on generalized complex geometry for physicists. Fortschr. Phys., 59(3- 4):169–242, 2011, https://proxy.library.spbu.ru:2150/doi/abs/10.1002/prop.201000083 • Maxim Zabzine. Lectures on generalized complex geometry and supersymmetry. Arch. Math. (Brno), 42(suppl.):119–146, 2006, https://www.emis.de/journals/AM/06-S/zabzine.pdf |