Открытые вопросы

Здесь собраны разнообразные нерешенные задачи о гиперболических многогранниках и связанных с ними объектах,

представляющие собой интерес.

Трудно заранее оценить их сложность (кроме задач программирования и визуализации). Совершенно неясно, каковы

ожидаемые ответы.

Задачи предлагаются всем желающим, но прежде всего -- студентам в качестве (сложной) курсовой или дипломной работы.

Задачи для школьников лежат здесь. (Примечание. Многие задачи уже решены.)

(Московская математическая конференция школьников)

Теоретические задачи

1. Охарактеризовать планарные графы, допускающие невыпуклое вложение в сферу.

Похоже, что эта задача слишком сложна. Поэтому я считаю разумным начать с более простого варианта:

2. Охарактеризовать все невыпуклые триангуляции сферы (т.е. все планарные графы, допускающие

невыпуклое вложение в сферу такое, что каждая область порожденного разбиения -- (сферический) треугольник.

Вот еще упрощение.

3. Привести пример планарного графа, не допускающего невыпуклого вложение в сферу

4. Всякий ли набор точек общего положения на сфере является множеством вершин некоторого ламан+1 невыпуклого

графа? (Набор точек таков, что всякая открытая полусфера содержит по крайней мере одну точку из набора.)

5. Всякий ли набор точек общего положения на сфере является множеством вершин некоторого правильно раскрашенного

трехвалентного невыпуклого графа ? Предполагается, что набор точек удовлетворяет следующему условию: всякая

открытая полусфера содержит по крайней мере одну точку из набора.

6. Известно, что всякая гладкая седловая сфера в $S^3$ (имеется ввиду вложенная поверхность,

гомеоморфная сфере), однолистно проецирующаяся на некоторую большую полусферу

имеет по крайней мере четыре больших дуги перегиба.

(а) Остается ли это утверждение верным, если убрать условие об

однолистной проекции

(б) Верно ли аналогичное утверждение для погруженных седловых

Поверхностей

(Примечание. Задача уже решена.)

7. Как известно, выпуклым многогранникам соответствуют очень обильные пучки

(имеется ввиду известное соответствие группа виртуальных

многогранников - группа Пикара торического многообразия). А что

соответствует гиперболическим виртуальным многогранникам

Задачи о приближении и сглаживании

1. Всякую ли кусочно-линейную седловую поверхность (скажем, в R^3) можно приблизить

седловой кусочно линейной поверхностью с дополнительным условием: из каждой вершины

выходит ровно три ребра(такие поверхности будем называть простыми)?

Стыдно, но до сих пор не решена следующая локальная версия этой задачи:

2.Задача решена. Рассмотрим седловую поверхность как на рисунке.

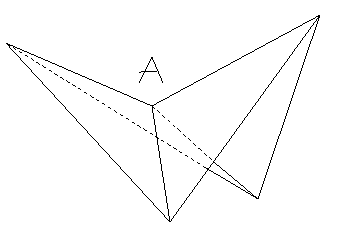
Можно ли вырезать некоторую окрестность точки А заклеить дырку кусочно-линейной

поверхностью так, чтобы полученная поверхность была седловой, простой и однолистно

проецировалась бы на некоторую плоскость?

Программирование и визуализация

1. Нарисовать 3D лифты (пока плоских) невыпуклых графов, возникающих

в первых работах о гиперболических многогранниках (это очень

просто). Должна получиться плоскость с нарисованным на ней графом

и кусочно-линейная поверхность, висящая над ней.

2. То же, что и в предыдущей задаче, но в глобальном виде (при

поворачивании мышкой картинка должно претерпевать проективные

преобразования)

3. Программа, вычисляющая

3D лифт вложенного в сферу ламан+1 графа (это известным образом сводится к решению

системы линейных уравнений) и строящая соответствующий виртуальный многогранник (как 3D объект).

4. Программа, строящая по набору точек на сфере все трехвалентные невыпуклые правильно раскрашенные графы с

вершинами в этих точках.

5. Программа, строящая по набору точек на сфере все ламан+1 невыпуклые графы с вершинами в этих точках..

6. Построение (3D) виртуального многогранника с 5 рогами и его веера.

7. Изгибание шарнирных механизмов на сфере. Задается изгибаемый шарнирный механизм на сфере со степенью свободы 1. Нужно

смоделировать его изгибание.