Summary of К.И. Пименов 'Алгебраическая перечислительная комбинаторика"

К.И. Пименов 'Алгебраическая перечислительная комбинаторика"
(ACC)

This course allows guest users to enter

К.И. Пименов 'Алгебраическая перечислительная комбинаторика"
(От species к теории представлений симметрической группы).

Первая лекция: 03.10.09 в 9-15 в ауд. 33 на 14 линии д.29.

Курс построен вокруг двух точек зрения на некоторый набор красивых комбинаторных формул.

Первый сюжет, которому будет посвящено три-четыре занятия, называется "Umbral calculus", он объясняет единым образом некоторые
соотношения для классических полиномиальных последовательностей.

Например, интерполяционная формула Ньютона из исчисления конечных разностей
$p(X)=\sum \frac {\Delta^kp(0)}{k!}X(X-1)\dots (X-k+1)$ ,
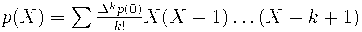оказывается прямым аналогом формулы Тейлора в некотором вполне строгом смысле,
связанном с переходом от стандартного мономиального базиса в пространстве многочленов к базису состоящему из многочленов
$\varphi_n(X)=X(X-1)\dots (X-n+1).$

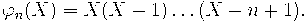
Биномиальная формула для этих многочленов
$\varphi_n(X+Y)=\sum{\rm C}_n^k \varphi_k(X) \varphi_{n-k}(Y)$
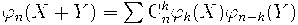
также легко объясняется без единой выкладки.
Хорошей иллюстрацией послужат и несколько классических соотношений между числами Стирлинга обоих родов и числами Бернулии.

Философский смысл "исчисления теней" опирается на наличие естественной структуры
коалгебры на кольце многочленов (коумножение задается биномом Ньютона).
Поэтому такая седая классика, как исчисление конечных разностей, оказывается провозвестником такой модной в последние десятилетия темы, как комбинаторные алгебры Хопфа, антипод одной из которых использован для ренормализации по Креймеру.
Впрочем вдаваться во всю эту высокую науку мы не будем.

Второй, основной сюжет, посвящен комбинаторным видам или типам структур --- таким, как
графы, деревья, упорядочения, разбиения на несколько частей, и задаче перечисления таких структур. В 1980 году A. Joyal предложил простое абстрактное понятие комбинаторного вида --- specie, конкретными примерами которых являляются понятия дерева и т.п.
Благодаря чему многие принципы перечислительной комбинаторики оказалось вомодным сформулировать в виде теорем.

Приведем два примера применения так называемого экспоненциального принципа.
Первый: пусть 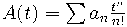$A(t)=\sum a_n\frac {t^n}{n!}$ --- производящая функция для числа деревьев с n вершинами. Тогда 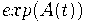$exp(A(t))$ --- это производящая функция для числа лесов (не обязательно связных графов без циклов).
Второй пример: 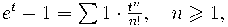$e^t-1=\sum 1\cdot\frac {t^n}{n!},\quad n\geqslant 1,$ --- это производящая функция для числа непустых множеств из n элементов
(по одному множеству для каждого n);
тогда 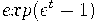$exp(e^t-1)$ --- это производящая функция для чисел разбиений n элементных множеств на несколько непустых частей.
Легко увидеть, что рассуждения, доказывающие оба факта, идентичны,
поэтому хочется сформулировать общую теорему, иллюстрацией которой эти факты служат: "производящая функция для числа несвязных структур равна экспоненте производящей функции от числа связных структур".
Благодаря Joyal'ю это утверждение сменило статус расплывчатого принципа на статус несложной теоремы.

Теорема перечисления Пойа про цикловой индекс действия группы на множестве
оказывается составной частью теории species.
Другой ключевой ингредиент --- полиномиальные функторы, по существу изобретенные И. Шуром еще в начале двадцатого века в связи с двойственностью Шура-Вейля между представлениями симметрических групп и полных линейных групп.
Поэтому не случайно, что познакомившись поближе species, мы с минимальными
услиями освоим базовые формулы из теории представлений симметрической группы.
Например, тот факт, что характеры неприводимых представлений --- это функции Шура, получится автоматически, практически без вычислений.

С примерной программой курса можно ознакомиться по адресу
www.math.spbu.ru/VAlgebra/SPECIES/exam211.pdf

Пререквизиты к этому курсу минимальны.
Требуется понимать про действие группы на множестве,
про переход от базиса к базису. К моменту начала разговора про species
хорошо бы ознакомиться с определением функтора и естественного преобразования на парочке примеров. Впрочем, никакая машинерия теории категорий использоваться не будет. Скорее наоборот, на рассматриваемые нами конкретные конструкции знаток теории категорий может смотреть как на примеры общих категорных конструкций (таких как расширение Кана и т.д.)
И наконец, к моменту начала изучения теории представлений симметрической группы,
полезно знать про соотношения ортогональности для характеров конечной группы.
Впрочем, аудитория при желании может заказать ликбез по теории представлений конечных групп.

Литература:

Я упомяну два учебника перечислительной комбинаторики общего плана:
M. Aigner "Enumeration theory" (см. www.math.spbu.ru/VAlgebra/SPECIES/Aigner.djvu)
и конечно же, "Перечислительную комбинаторику" Р. Стэнли.

по Umbral Calculus и биномиальным последовательностям:
глава 4 книги www.math.spbu.ru/VAlgebra/SPECIES/RotaWay.pdf
и заметка Кнута www.math.spbu.ru/VAlgebra/SPECIES/KnuthCon.pdf

По species:
книга "Combnatorial species and tree like structures" www.math.spbu.ru/VAlgebra/SPECIES/Species.djvu,
и более продвинутый курс лекций одного из авторов этой книги,
в котором излагается и введение в теорию представлений симметрической группы
www.math.spbu.ru/VAlgebra/SPECIES/bergeron.pdf

К.И. Пименов 'Алгебраическая перечислительная комбинаторика"(ACC)

К.И. Пименов 'Алгебраическая перечислительная комбинаторика"
(ACC)