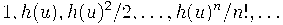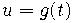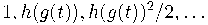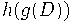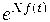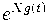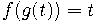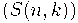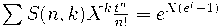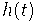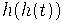Матрица Паскаля как линейный оператор на формальных степенных рядах оказывается умножением на
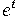
, так что биномиальная формула обращения
следует из тождества
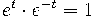
.
Линейные функционалы на пространстве
![\mathbb C[X] \mathbb C[X]](http://club.pdmi.ras.ru/moodle/filter/tex/pix.php/4f111e1973b689349a51ed106bda9a1a.gif)
, их отождествление
с формальными степенными рядами
![\mathbb C[[t]] \mathbb C[[t]]](http://club.pdmi.ras.ru/moodle/filter/tex/pix.php/bdbf86fa3a7e2f333dffb34b4770448a.gif)
по правилу
![f(t)\mapsto \left[p(X)\mapsto f\left(\left.\frac \partial{\partial X}\right)p(X)\right|_{X=0}\right] f(t)\mapsto \left[p(X)\mapsto f\left(\left.\frac \partial{\partial X}\right)p(X)\right|_{X=0}\right]](http://club.pdmi.ras.ru/moodle/filter/tex/pix.php/d8b864552cf8242503883c9f6fb36bcc.gif)
.
Примеры: Значению в нуле отвечает ряд
![1\in\mathbb C[[t]] 1\in\mathbb C[[t]]](http://club.pdmi.ras.ru/moodle/filter/tex/pix.php/a8b28d72c5dc28a0b0b75b7d1246c498.gif)
,
значению в точке
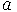
отвечает ряд
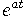
.
Функционалу
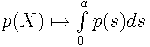
отвечает ряд
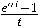
.
"Базис" в
![\mathbb C[[t]] \mathbb C[[t]]](http://club.pdmi.ras.ru/moodle/filter/tex/pix.php/bdbf86fa3a7e2f333dffb34b4770448a.gif)
, двойственный к мономиальному базису в
![\mathbb C[X] \mathbb C[X]](http://club.pdmi.ras.ru/moodle/filter/tex/pix.php/4f111e1973b689349a51ed106bda9a1a.gif)
, --- это

Оператор умножения на
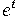
в пространстве формальных степенных рядов
оказывается сопряженным к оператору сдвига на пространстве многочленов.
Вообще, оператор умножения на
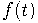
оказывается сопряженным оператору
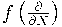
.
Снова о биномиальных последовательностях.
Вывод из определения 1 определения 3 (решение функционального уравнения
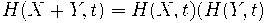
).
Вывод определения 2 из определения 3 --- применением оператора
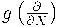
, где
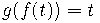
,
к равенству
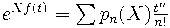
.
Иллюстрация: для биномиальной последовательности нижних факториалов
отвечающей дельта-оператору
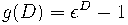
получаем формулу бинома Ньютона:
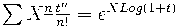
,
т.е.
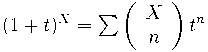
.
Композиция биномиальных последовательностей.
Теорема.Умножению матриц коэффициентов двух биномиальных последовательностей многочленов соответствует подстановка ряда в ряд.
Доказательство:
Рассмотрим биномиальную последовательность
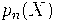
отвечающую дельта оператору
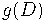
, т.е.
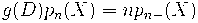
. Тогда "базис" в
![C[[t]] C[[t]]](http://club.pdmi.ras.ru/moodle/filter/tex/pix.php/31a5f6dfe8010f4f8700812b9c9ca708.gif)
, двойственный к базису
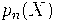
, --- это
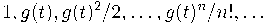
,
то есть получается из "стандартного базиса" подстановкой
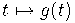
.
Пусть
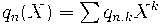
--- биномиальная последовательность, отвечающая оператору
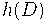
.
Тогда матрицу
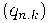
можно трактовать как матрицу перехода
от базиса
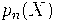
к базису
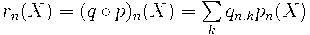
(напомним, что базис в пространстве
![\mathbb C[X] \mathbb C[X]](http://club.pdmi.ras.ru/moodle/filter/tex/pix.php/4f111e1973b689349a51ed106bda9a1a.gif)
мы записываем столбцом).
Значит
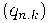
--- это матрица перехода от "базиса"
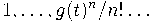
в
![\mathbb C[[t]] \mathbb C[[t]]](http://club.pdmi.ras.ru/moodle/filter/tex/pix.php/bdbf86fa3a7e2f333dffb34b4770448a.gif)
к базису, который двойственен
к
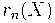
(если выписывать "базисы" в
![C[[t]] C[[t]]](http://club.pdmi.ras.ru/moodle/filter/tex/pix.php/31a5f6dfe8010f4f8700812b9c9ca708.gif)
в строчку).
Но мы знаем, что базис

, где
![u\in \mathbb C[[t]] u\in \mathbb C[[t]]](http://club.pdmi.ras.ru/moodle/filter/tex/pix.php/0f0b584099b1eaf6ee0259c73861ab9c.gif)
переводится умножением на матрицу
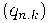
в
базис
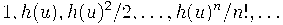
. Беря
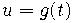
мы видим,
что базис, двойственный
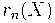
--- это
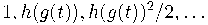
.
Таким образом,
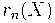
--- биномиальная последовательность,
отвечающая дельта-оператору
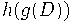
.
К примеру, если две биномиальные последовательности многочленов
имеют производящие функции
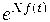
и
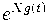
такие, что
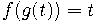
, то соответствующие матрицы коэффициентов взаимно обратны.
Иллюстрация:
матрица из чисел Стирлинга второго рода
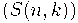
,
будучи обратной к матрице перехода от мономиального базиса к нижним факториалам имеет экспоненциальную производящую функцию
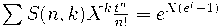
.
Замечательное практическое следствие доказанной теоремы состоит
в том, что композицию двух аналитических функций в окрестности нуля
можно вычислять перемножая отвечающие им матрицы.
Более того, при помощи умножения таких матриц можно написать формулу
для извлечения "композиционного квадратного корня", т.е. найти ряд
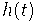
такой, что
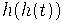
равен наперед заданному формальному степенному ряду.

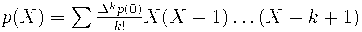
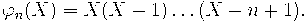
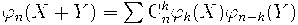
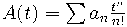
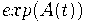
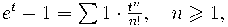
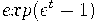
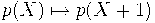
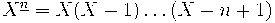
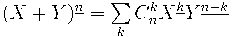

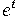
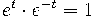
![\mathbb C[X] \mathbb C[X]](http://club.pdmi.ras.ru/moodle/filter/tex/pix.php/4f111e1973b689349a51ed106bda9a1a.gif)
![\mathbb C[[t]] \mathbb C[[t]]](http://club.pdmi.ras.ru/moodle/filter/tex/pix.php/bdbf86fa3a7e2f333dffb34b4770448a.gif)
![f(t)\mapsto \left[p(X)\mapsto f\left(\left.\frac \partial{\partial X}\right)p(X)\right|_{X=0}\right] f(t)\mapsto \left[p(X)\mapsto f\left(\left.\frac \partial{\partial X}\right)p(X)\right|_{X=0}\right]](http://club.pdmi.ras.ru/moodle/filter/tex/pix.php/d8b864552cf8242503883c9f6fb36bcc.gif)
![1\in\mathbb C[[t]] 1\in\mathbb C[[t]]](http://club.pdmi.ras.ru/moodle/filter/tex/pix.php/a8b28d72c5dc28a0b0b75b7d1246c498.gif)
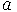
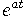
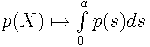
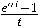

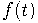
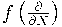
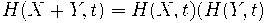
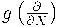
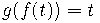
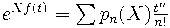
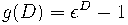
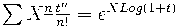
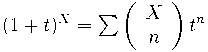
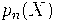
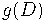
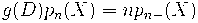
![C[[t]] C[[t]]](http://club.pdmi.ras.ru/moodle/filter/tex/pix.php/31a5f6dfe8010f4f8700812b9c9ca708.gif)
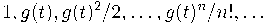
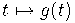
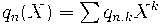
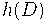
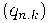
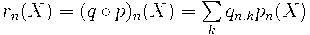
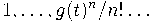
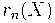

![u\in \mathbb C[[t]] u\in \mathbb C[[t]]](http://club.pdmi.ras.ru/moodle/filter/tex/pix.php/0f0b584099b1eaf6ee0259c73861ab9c.gif)