| |
 Новостной форум Forum Новостной форум Forum- Первая лекция 26.09.09 13:30 ауд 311 ПОМИ
Со времен Эйлера известны различные способы суммировать не обязательно сходящиеся ряды. Например, можно вместо предела частичных сумм 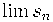 расмотреть предел чезаровских средних расмотреть предел чезаровских средних  . Это позволяет определить ``сумму'' ряда . Это позволяет определить ``сумму'' ряда 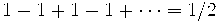 .Часто возникают ситуации, при которых удается получить как раз такую более слабую, чем классическая сходимость, информацию о рядах, интегралах, асимптотиках функций и пр. Оказывается, что при некоторых дополнительных предположениях можно утверждать, что имеет место и более сильная, классическая сходимость. Например, в примере выше если .Часто возникают ситуации, при которых удается получить как раз такую более слабую, чем классическая сходимость, информацию о рядах, интегралах, асимптотиках функций и пр. Оказывается, что при некоторых дополнительных предположениях можно утверждать, что имеет место и более сильная, классическая сходимость. Например, в примере выше если 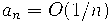 или хотя бы или хотя бы 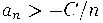 , то ряд , то ряд 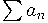 , сходящийся по Чезаро, сходится в классическом смысле. Это тауберова теорема Харди-Ландау, а первая была придумана Альфредом Таубером в 1897 году. В XX веке развитие тауберовой теории связано с именами Харди, Литтлвуда, Винера, Караматы. В значительной степени стимулом к развитию теории послужила арифметика (закон распределения простых чисел и далее). Непосредственная часть имеется также с банаховыми алгерами и топологическими группами. В статистической физике тауберовы теоремы помогают переходить от результатов о так называемом ``большом каноническом ансамбле'' к ``'малому''. Эта аналогия позволила А. М. Вершику получить асимптотические результаты о больших комбинаторных объектах, распределенных случайно согласно некоторым (вполне естественным) мерам. , сходящийся по Чезаро, сходится в классическом смысле. Это тауберова теорема Харди-Ландау, а первая была придумана Альфредом Таубером в 1897 году. В XX веке развитие тауберовой теории связано с именами Харди, Литтлвуда, Винера, Караматы. В значительной степени стимулом к развитию теории послужила арифметика (закон распределения простых чисел и далее). Непосредственная часть имеется также с банаховыми алгерами и топологическими группами. В статистической физике тауберовы теоремы помогают переходить от результатов о так называемом ``большом каноническом ансамбле'' к ``'малому''. Эта аналогия позволила А. М. Вершику получить асимптотические результаты о больших комбинаторных объектах, распределенных случайно согласно некоторым (вполне естественным) мерам.
Мы планируем обсудить основные тауберовы теоремы, их приложения к арифметике и подробно остановиться на предельных формах больших комбинаторных объектов.
Желательно знание основ вещественного и комплексного анализа и классического преобразования Фурье.
Литература.
1. Г.Х. Харди. Расходящиеся ряды.
2. J. Korevaar. Tauberian Theory. A century of developments
3. А. М. Вершик. Статистическая механика комбинаторных разбиений и их предельные конфигурации, Функц. анализ и его прил., 30:2 (1996)
| |