| | |
Евгений Степанов, ПОМИ РАН и Пизанский университет (Италия)
Занятия по средам с 28.01 с 10.00 до 12.50 МСК, ОНЛАЙН в ZOOM Просьба регистрироваться на сайте и на телеграм канале курса.
Аннотация.
Целью курса является ввести слушателей в круг основных современных идей и приложений, развивающихся вокруг классической задачи об оптимальном переносе массы, сформулированной более 200 лет назад Г. Монжем. Как оказалось, эта задача является весьма глубокой, а разработанные для ее решения инструменты находят свое применение в самых разных областях математики, в частности, в дифференциальной геометрии, метрической геометрии, теории вероятностей, уравнениях в частных производных, геометрической теории меры.
Курс полезен не только математикам, но и гораздо более широкому кругу специалистов, в частности, физикам и информатикам. Однако материал курса достаточно продвинутый и требует от слушателей хороших рабочих знаний вещественного анализа и линейной алгебры, а также основ теории вероятностей / теории меры и функционального анализа (а желательно еще и римановой геометрии или по крайней мере геометрии кривых и поверхностей).
Примерный набор тем.
1. Классическая задача Монжа. Ослабленная формулировка Канторовича. Вероятностная интерпретация. Квадратичная и линейная задачи. Двойственные формулировки. Транспортный потенциал. [Приложения: изопериметрическое неравенство и/или другие неравенства.]
2. Связь с уравнениями в частных производных (с разной степенью подробности, возможно – только обзорно: теория Y.Brenier – уравнение неразрывности; уравнение переноса массы; уравнение Монжа-Ампера). Транспортная плотность.
3. Существование решений задачи Монжа (решение квадратической задачи, решение линейной задачи в одномерном случае, основная идея решения линейной задачи в общем случае).
4. Метрика Канторовича (Вассерштайна). Пространства мер с метрикой Канторовича. Касательный формализм и displacement convexity. Пространство мер с расстоянием Канторовича как многообразие. Градиентные потоки и минимизирующие движения. [Otto calculus и приложения к уравнениям математической физики.] [Энтропийная регуляризация]
5. [Сети оптимального переноса массы].
Потоки Уитни, основные понятия. Дробные массы. Ветвящиеся транспортные сети. Метрики Канторовича (Вассерштайна) с дробными показателями. [Задача оптимальной ирригации. Регулярность оптимальных сетей.] |
| |
Б.Б. Шойхет
Теория гомотопий и алгебраическая К-теория
Курс Физматклуба - EIMI, осень 2025, ПОМИ, Zoom. Сайт курса на Indico. Желающих участвовать просьба: 1. Зарегистрироваться на Indico, 2. Подписываться на Телеграм-канал
В прошлом семестре мы разобрали некоторые сюжеты, так или иначе связанные с распетливанием и алгебраической К-теорией: 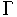 -пространства Сигала, групповое пополнение несвязных топологических моноидов, плюс-конструкцию Квиллена и Q-конструкцию. Это приводит к нескольким определениям высшей алгебраитческой K-теориии.
В этом семестре планируется углубиться в эту тематику. Мы разберем совпадение определений K-теории через плюс- и Q-конструкции и докажем фундаментальные теоремы Квиллена. Также мы обсудим К-теорию Вальдхаузена и ее связь с Q-конструкцией, что открывает новые возможности, связанные с использованием слабых эквивалентностей. Планируется такжеобсудить отдельные более явные сюжеты, такие как K2 от поля, некоторые вычисления высших K-групп, и связи с алгебраической геометрией. Очень желательно некоторое знакомство с тем что было в прошлом семестре.
Литература:
Quillen, Higher Algebraic K-theory, LNM 341
Grayson, Higher Algebraic K-theory II (after Quillen)
Милнор, Введение в алгебраическую К-теорию Srinivas, Algebraic K-theory |
| |
И.А. Панин
Теория схем Гротендика
Начало 12-го сентября 2025 г. в 18.00, ПОМИ к. 203. Желающих участвовать просьба регистрироваться.
Цель курса - познакомить слушателей с красивейшей теорией, теорией схем Гротендика, теорией, преобразившей алгебраическую геометрию. Пред схема, подобно всём геометрическими объектам с дополнительной структурой - это топологическое пространство Х, снабжённое пучком колец O. Их характерное свойство - наличие такого открытого покрытия {U_i} , что {U_i, O ограниченный на U_i} - это одна из стандартных предсхем вида Spec A, где А - коммуникативное кольцо с единицей. Категория аффинных схем (схем типа Spec A) эквивалентна категории коммутативных колец с единицей (с обращёнными стрелками). В категории предсхем всегда есть расслоенные произведения, причём расслоенное произведение Spec A и Spec B над Spec C это Spec (A tensor B), tensor над С. Наличие расслоенного произведения позволяет делать такие операции, как расширить скаляры от поля k до поля К, определить понятие схемного слоя морфизма f: X --> Y над точкой y из Y, определить понятие групповой пред схемы Х над S. В частности, для S =Spec (Bbb Z) ввести классические групповые схемы над Вb Z: GL_n, SL_n, PGL_n, O_n, SO_n, Sp_2n Определить проективное пространство P^n над S и описать всё морфизмы (над S) из S- пред схемы X в P^n_S. Проективное пространство над S это схема типа Proj (R), где R - градуированное коммутативное кольцо. Частными случаями этой конструкции являются Грассманианы (над S), раздутия схемы вдоль замкнутой под схемы и ... . Содержательная теория схем невозможна без обсуждения когерентных пучков и их когомологий. Курс будет следовать 3-м книгам:
[1] Д. Мамфорд. Лекции о кривых на алгебраической поверхности (лекции 3--11)
[2] Ю. И. Манин. Введение в теорию схем и квантовые группы.
[3] Р. Хартсторн. Алгебраическая геометрия |
| |
В осеннем семестре 2025 года планируется продолжить изучение основ квантовой теории поля. В рамках основной программы будут рассмотрены такие понятия, как расходимость, регуляризация, сингулярность и перенормировка. Особое внимание будет уделено анализу конкретных примеров с проведением детальных вычислений.
Занятия планируется начать с октября. Семинары будут проводиться в офлайн-формате в ПОМИ РАН. День недели будет согласовываться с участниками для удобства. За дополнительной информацией и вопросами обращайтесь по электронной почте regul1@mail.ru. Также вы можете запросить ссылку на Telegram-канал. |
| |
С. Ягунов
Пучки и когомологии в алгебраической геометрии.
Курс, будет читаться по вторникам с 19 часов в 311 ауд ПОМИ Первое занятие 9 сентября. Сайт курса. Заитересованных просьба регистрироваться
В прошлом семестре мы поговорили об основных понятиях современной алгебраической геометрии таких, как алгебраические многообразия, схемы и пучках на них, а также немного о гротендиковском подходе к геометрии --- способах задания топологий в алгебро-геометроическом контексте. Мы продолжим изучение схем, сделав в этом семестре больший акцент на когомологиях пучков. Соответственно, мы планируем поговорить и о разных топологиях. Начав с когомолоий пучков в топологии Зарисского, мы постепенно перейдем к такому важному предмету, как этальные когомологии. В перспективе мы планируем обсудить появившийся в последние десятилетия подход к алгебраической геометрии, используюший понятия мотивов и А^1-спектров, представляющих различные теории когомологий на схемах. Данный курс является продолжением читавшегося в прошлом семестре курса "Когомологии в алгебраической геометрии", а также, в некотором более слабом смысле, курсов 2024 года "Пучки и их когомологии" и "Основы гомотопической алгебры", однако я буду рад видеть также и слушателей, не посещавших этих курсов. При необходимости я собираюсь провести несколько дополнительных лекций, на которых рассказать вкратце необходимый материал. Также (почти) все лекции этих курсов могет быть найдены здесь https://yagunov.info/Courses/Courses.html |
| |
Семинар "Геометрия и комбинаторика" возобновляет свою работу и приглашает младшекурсников. Наша локальная цель в этом семестре -- выучить необходимые пререквизиты о слоениях и контактных структурах. Сайт семинара. Желающих участвовать просьба регистрироваться .
Первое занятие состоится 9 сентября, в 9-30, на 14 линии, ауд. 120. |
| |